1. Intuition
决策树是一种分类算法,其模型为树结构
每个非叶节点代表一个测试,而每个叶节点都与一个类别相关
其对单个样本的分类过程从最上的根节点开始,根据测试结果往下走,直到走到叶节点
这样这个样本就被决策树预测了类别,一个例子如下
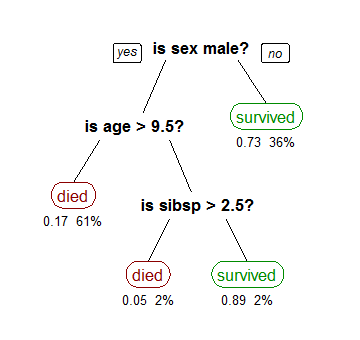
2. 构建流程
大部分决策树构建算法都是自顶向下构建的
根节点处理全部的数据,并将其划分为多个子集,传给其子节点
子节点处理其接收到的数据,再次划分,这样递归下去完成决策树的构建
其单个节点的构建详细流程如下
- 接收本节点的数据D
- if D中所有的数据都是一个类别
- 将本节点设定为叶节点,并将其类别标注为的类别
- 结束
- 使用某种分裂规则将D划分为若干个子集
- 对所有的子集
- 创建子树
某种分裂规则是指选择某个特征,并以该特征的值作为划分数据子集的依据
通常这种准则,应使得各个子集尽可能只有一个类别
3. 分裂规则
这里介绍三个比较常见的分裂依据,分别为信息增益、增益率、基尼指数
设数据中的类别有个,第个类别以表示
是中类数据的集合
3.1 信息增益
ID3使用信息增益作为分裂依据
数据D的熵为
\begin{align} Entropy(D) = -\sum_{i=1}^mp_i\log_2(p_i) \end{align}
表示类别在数据中的概率,可以设定为
\begin{align}p_i=\frac{|C_{i,D}|}{|D|} \end{align}
假定选择特征对数据进行划分
先假定是离散特征,在数据中的所有可能取值有个,第个取值为
于是很自然地划分出个子集,第个子集称为
划分后的熵可以定义为
\begin{align} Entropy_A(D) = \sum_{j=1}^v\frac{|D_j|}{|D|}Entropy(D_j) \end{align}
信息增益定义为
\begin{align} Gain(A) = Entropy(D) - Entropy_A(D) \end{align}
显然,表示通过划分,不确定性减少的程度
于是我们要选择使得信息增益最大的特征进行划分
上面考虑的是A是离散值的情况下
实际上,在A是连续值的情况下,在分裂时是选择一个阈值
特征的值小于等于阈值的划分为一个子集,大于阈值的划分为另一个子集
3.2 增益率
ID3有一个缺点,倾向于划分出更多的子集。
极端情况下,将数据D划分为一条数据一个子集,但是这种划分对于分类并没有用
C4.5是ID3的后继者,引入一个参数用于改善这种缺点
引入一个称为split information的值
对特征A做划分的split information为
\begin{align} SplitInfo_A(D) = -\sum_{j=1}^v\frac{|D_j|}{|D|}\log_2\left(\frac{|D_j|}{|D|}\right) \end{align}
容易发现,这其实是个熵,划分出的子集个数越多,这个split information越大
而增益率定义为
\begin{align} GrainRate(A) = \frac{Gain(A)}{SplitInfo_A(D)} \end{align}
选择最大增益率的特征进行分裂,这种方法就是C4.5
3.3 基尼指数
CART使用基尼指数作为划分依据
基尼指数度量数据D的不纯度(数据纯意味这所有数据都是一个类别)
\begin{align} Gini(D) = 1 - \sum_{i=1}^mp_i^2 \end{align}
CART对于离散值和连续值特征都是划分为两个子集
设划分为两个子集和
划分后的基尼指数设定为
\begin{align} Gini_A(D) = \frac{|D_1|}{|D|}Gini(D_1) + \frac{|D_2|}{|D|}Gini(D_2) \end{align}
选择最小的特征进行分裂,这种方法就是CART