1. Generative model
LDA的贝叶斯网络表示
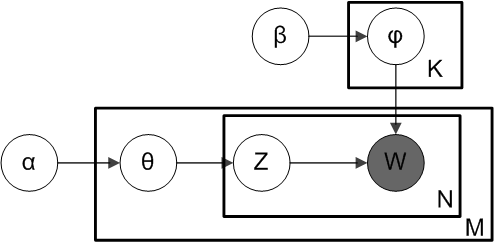
符号意思为
- :文档数量
- :所有文档出现的词组成的词表的大小
- :总词数,为所有文档的词数的总和
- :主题数量
- :文档,表示第篇文档
- :词,表示的第个词,表示的个词
- :主题,表示第个主题
- :所有文档的所有词组成的维向量
- :所有文档的所有词对应的主题组成的维向量
- :为多项式分布的参数,表示
- :
- :的先验分布(Dirichlet分布)的参数
- :为多项式分布的参数,表示
- :
- :的先验分布(Dirichlet分布)的参数
2. The collapsed LDA Gibbs sampler
2.1 The joint distribution
在LDA中,由贝叶斯网络可以得到如下分解
\begin{align} p(W,Z\vert \alpha,\beta)=p(W\vert Z,\beta)p(Z\vert \alpha) \end{align}
为了符号简洁,定义
\begin{align} \Delta (\alpha) = \frac{\prod_{i}\Gamma(\alpha_i)}{\Gamma(\sum_i\alpha_i)} \end{align}
上式中的第一项进行化简
\begin{align} p(W\vert Z,\beta) &=\int p(W\vert Z,\Phi)p(\Phi\vert \beta)d\Phi \\ &= \int p(\Phi\vert \beta)\prod_{k=1}^K\prod_{t=1}^V\varphi_{k,t}^{n_{k,t}}d\Phi \\ &= \prod_{k=1}^K\frac{\Delta(n_k+\beta)}{\Delta \beta},\quad n_k={n_{k,t}}_{t=1}^V \end{align}
化简第二项
\begin{align} p(Z\vert \alpha)&=\int p(Z\vert \Theta)p(\Theta\vert \alpha)d\Theta \\ &=\int p(\Theta\vert \alpha)\prod_{m=1}^M\prod_{k=1}^K\theta_{m,k}^{n_{m,k}}d\Theta \\ &=\prod_{m=1}^M\frac{\Delta(n_m+\alpha)}{\Delta(\alpha)},\quad n_m={n_{m,k}}_{k=1}^K \end{align}
于是联合概率分布为
\begin{align} p(Z,W\vert \alpha,\beta)=\prod_{k=1}^K\frac{\Delta(n_k+\beta)}{\Delta \beta}\prod_{m=1}^M\frac{\Delta(n_m+\alpha)}{\Delta(\alpha)} \end{align}
2.2 Full conditional
令表示第篇文档的第个词 求
\begin{align} p(Z_i=k\vert Z_{\neg i},W)&=\frac{p(W,Z)}{p(W,Z_{\neg i})} \\ &=\frac{p(W\vert Z)}{p(W_{\neg i}\vert Z_{\neg i})p(W_i)}\frac{p(Z)}{p(Z_{\neg i})} \\ &\propto \frac{\Delta(n_k+\beta)}{\Delta(n_{k,\neg i}+\beta)}\frac{\Delta(n_m+\alpha)}{\Delta(n_{m,\neg i} + \alpha)} \end{align}
不断进行采样,即可得到
2.3 Multinomial parameters
最后我们需要得到和
\begin{align} p({\theta}_m\vert {\alpha},W,Z)&=\frac{1}{Norm}\prod_{n=1}^{N_m}p(Z_{m,n}\vert {\theta}_m)p({\theta}_m\vert {\alpha})=Dir({\theta}_m\vert {n}_m+{\alpha}) \\ p({\varphi}_k\vert {\beta},W,Z)&=\frac{1}{Norm}\prod_{i:Z_i=k}p(W_i\vert {\varphi}_k)p({\varphi}_k\vert {\beta})=Dir({\varphi}_k\vert {n}_k+{\beta}) \end{align}
容易发现,这个结果使得在线学习非常容易 使用Dirichlet分布的期望就是最后的结果了