Feedforward Neural Network

神经网络作为机器学习的一个重要分支，在业界的应用非常广泛

本文介绍下其中最简单的Feedforward Neural Network（下文简称FNN）

下图是一个典型的3层FNN

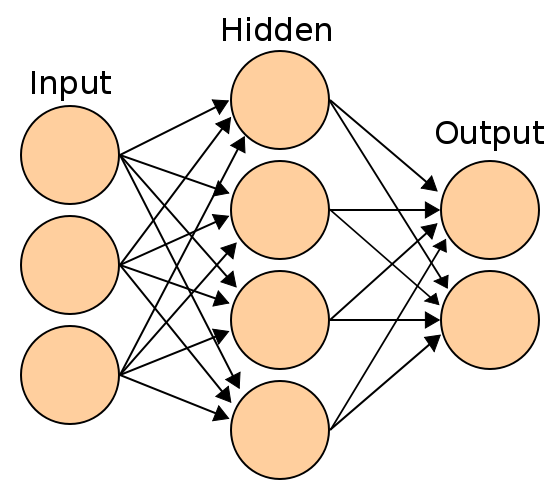
每个圆圈称为一个神经元，上图分为输入层，隐层，输出层

实际场景下，隐层往往不止一个，而且也不是和上图一样的全连接

设定输入层有$n$个神经元（对应Feature），输出层有$k$个神经元（对应Label）

则神经网络拟合的是一个函数关系$R^n \rightarrow R^k$

神经网络中每一个隐层神经元和输出层神经元对于前一层传来的数据会进行如下计算然后传给下一层（输出层结果就是模型预测结果）

\begin{align} output = g(\theta^T input) \end{align}

$g$为激活函数，每个神经元的激活函数可能都不一样（但通常每层是一样的）

$\theta$为参数，是一个与前一层输出同维度的向量，对应于图中的边，由训练过程得到

通常每层第一个是Bias神经元，但也可以没有

其梯度$\theta$的计算式子可以通过链式求导得到，之后使用梯度下降法/牛顿法或其他方法均可求解

公式上非常简单的模型，却有着非常强大的拟合能力

在全连接的FNN中，每一层的作用可以视为一个线性变换+激活，正是激活函数的存在使其具有强大的拟合能力，同时也变得难以解释（相应的数学工具缺失）。

接下来我们推导一下其梯度（为了方便，不考虑Bias，只考虑全连接）

$a^l$表示第$l$层的激活向量，$z^l$表示第$l$层的激活前的向量，则有

\begin{align} a^{l+1} =g(z^{l+1})= g(\theta^la^l) \end{align}

使用$d^l$表示第$l$层的维数，则$\theta^l \in R^{d^{l+1}*d^l}$

设损失函数为$J(\theta)$，有

\begin{align} \frac{\partial J}{\partial \theta^l} = \frac{\partial J}{\partial z^{l+1}}\frac{\partial z^{l+1}}{\partial \theta^{l}}=\frac{\partial J}{\partial z^{l+1}}(a^l)^T \end{align}

定义符号$\delta^{l} =\frac{\partial J}{\partial z^{l}}$

则有 \begin{align} \frac{\partial J}{\partial \theta^l}=\delta^{l+1}(a^l)^T \end{align}

上式中还有$\delta^{l+1}$需要求解

因为

\begin{align} \delta^l &= \frac{\partial J}{\partial z^{l}} \\ &= \frac{\partial J}{\partial z^{l+1}}\frac{\partial z^{l+1}}{\partial a^{l}}\frac{\partial a^{l}}{\partial z^{l}} \\ &= ((\theta^l)^T\delta^{l+1}) \cdot g’(z^l) \end{align}

梯度反向传播的框架到这里已经很清晰了，从最后一层开始，逐层计算$\delta^l$，并计算对应的梯度