本文翻译自Why are deep neural networks hard to train? 。精简了一下,不保证完全一致,仅供参考。
1. 引言
假设你是一个工程师,被要求从头开始设计一个计算机。并且customer提出了一个要求:整个计算机的电路必须是2层深。如图

这是个crazy的需求,但并不是不可能。因为两层深的电路已经可以完成任何函数的计算(如不了解,查看这篇文章,不理解不影响继续往下看,只需要记住这个结论)。
但是能做到并不意味着没有缺点。在实践中,在解决电路设计问题(或者大部分的算法问题)时,我们通常会从解决子问题开始,然后一步步地整合子问题从而得到原始问题的解法。换句话说,我们经过多层的抽象才得到一个解决方案。
举个例子,假如我们需要设计一个逻辑电路来计算两个数的乘法。首先,我们会建立子电路来做两个数的加法。设计这个加法电路时,我们同样又会设计子电路来做两个bit的加法。如图:

最终,我们的电路至少有三层。
深层电路使得程序设计更加简单,但其意义不止如此。数学上已经证明,对于某些函数,相比深层电路,使用浅层电路进行计算需要多耗费指数数量的电路元件。
在1980年代的一系列paper已经证实了,使用浅层电路做奇偶校验需要耗费指数级的门电路。而另一方面,如果使用深层电路,则只需要少量的电路就可以完成计算,只需要bit之间两两计算奇偶,然后使用上一层的结果继续两两计算奇偶,最终完成计算。
由此可见,深层电路比浅层电路更加强大。 回到神经网络的问题中,我们先看单隐层网络。如图

这种简单的网络非常实用,使用其来处理MNIST数据可以达到98%的准确率。然而,我们还是希望使用更多的隐层,使其更加强大。

这种网络使用中间层来建立多层抽象。比如,如果是视觉模式识别,第一层的神经元可能是识别边,第二层的神经元可能是识别更复杂的形状(比如说三角形),第三层可能是识别更加复杂的形状。多层抽象使得深度网络在解决复杂模式识别的问题上有强大的优势。
接下来,我们要谈谈如何训练这样的深度网络。我们先使用SGD反向传播来尝试一下,稍后我们会发现,这样训练出来的深度网络效果并不比浅层网络好。
这个效果显然不符合我们之前讨论的结果,之后我们要去探讨为什么会变成这样。更进一步地观察,我们会发现深度网络中不同的层的学习速率极不一样。准确地说,后层(later layer)学习地很快很好,而前层(early layer)的学习会进入困境,很慢,甚至几乎什么都没学习到。这个困境并不是巧合,其与我们基于梯度的学习方法有关。
2. 梯度消失问题
我们首先回顾单隐层网络。
这里我们使用MNIST作为实验数据,进行实际的训练操作。
准备好Python2.7, Numpy
然后下载代码
git clone https://github.com/mnielsen/neural-networks-and-deep-learning.git
进入源码目录后运行Python Shell读取MNIST数据
>>> import mnist_loader
>>> training_data, validation_data, test_data = \
... mnist_loader.load_data_wrapper()
设置网络结构
>>> import network2
>>> net = network2.Network([784, 30, 10])
输入层784个neuron对应于输入图像的784个像素,单隐层30个neuron,输出层10个neurons对应于10个分类结果。
我们使用10个样本作为一个mini-batches,设定学习率0.1,设定regularization参数为5.0,迭代30轮。训练过程中,我们打印验证集上的分类准确率。
>>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, \
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)
运行可得到96.48%的分类准确率(实际运行会有细微差别,不必在意)
现在,我们加一个同样30个neuron的隐层,使用同样的超参数来训练
>>> net = network2.Network([784, 30, 30, 10])
>>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0, \
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)
这次会得到一个更好的分类准确率:96.90%。可以看到,多一点点的深度可以有更好的效果。
现在,我们再加一个同样大小的隐层。
>>> net = network2.Network([784, 30, 30, 30, 10])
>>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0,
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)
这一次,我们得到96.57%的准确率。可以看到,这回添加的隐层没有产生任何作用。
我们继续加隐层
>>> net = network2.Network([784, 30, 30, 30, 30, 10])
>>> net.SGD(training_data, 30, 10, 0.1, lmbda=5.0,
... evaluation_data=validation_data, monitor_evaluation_accuracy=True)
这一回的分类准确率是96.53%,分类准确率又一次下降。
这看起来很诡异,额外的隐层应该会使得网络可以学习更加复杂的分类函数,然后可以更好的分类。并且,额外的隐层也不应使得结果更加糟糕,因为最坏的情况下,额外的隐层可以什么都不做。
为什么会变成这样呢?我们可以认为额外的隐层的确对网络有提升,但问题是我们的学习算法没有找到正确的weight和bias。
为了确认哪里出的问题,我们选取两个隐层的网络,也就是[784,30,30,10],对其训练过程做一些观察工作。如图
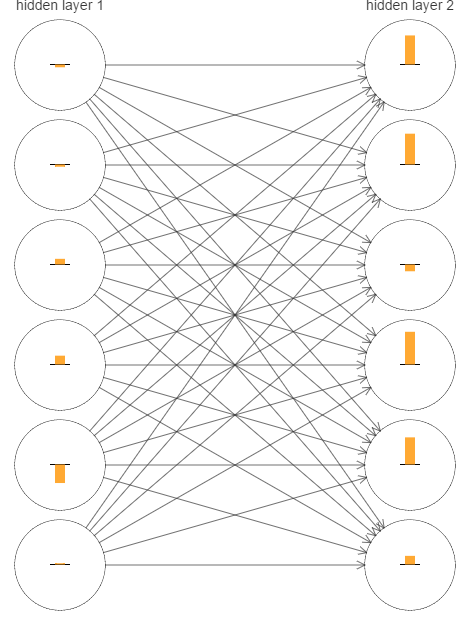
图中的每个neuron有一个黄条,这个neuron对应的weight和bias变化越快,这个条越大。更正式的说法是,这个条代表了每个neuron的梯度大小。
为了简洁,只选择两个隐层最上面的6个neuron进行展示。
图中的条代表的是在训练初期,也就是网络刚完成初始化后的训练。
网络是被随机初始化的,所以各个neurons学习速度不一致符合预期。然而,从图中,还是能发现一个普遍规律,第二隐层的条大部分都比第一隐层的大很多。所以,第二隐层的学习速度会比第一隐层快很多。
我们需要确认这是不是一个巧合。
使用表示第层的第个neuron的梯度
那么,是一个向量,用于表示第一隐层的学习速度。同样,表示第二隐层的学习速度。
那么,向量长度就反映了隐层的整体学习速度。
通过计算可以得到,而
这个结果证明了之前的结论,第二隐层的学习速度的确比第一隐层快
我们继续增加隐层进行观察,在[784,30,30,30,10]网络结构中,隐层的学习速度分别为0.012,0.060和0.283。再加一层,我们会得到0.003,0.017,0.070和0.285。
之前都是在讨论训练初期,现在我们看看完整过程中训练速度的变化趋势。 仍然是双隐层,如图

为了生成这个结果,我使用1000个训练图像训练了500轮,并且这次没有使用mini-batch。
可以看到,在这张图的所有情况下,第一隐层的学习速度都要比第二隐层慢。
再新增一个隐层的结果如下

最后,我们再加一个隐层

再一次验证了之前的结论,越是前面的层,学习速度越慢。从图中可以看出,第一隐层的学习速度比最后一层的学习速度慢100多倍。
这种现象称为梯度消失,前层的梯度比后层小,在有些时候,会出现完全相反的情况,前层的梯度比后层大,这又称为梯度爆炸。当然,梯度爆炸,也不是什么好情况。
这种现象说明深度神经网络中的梯度并不稳定,我们需要理解其发生的原因,并解决。
在此之前,我们需要知道梯度消失是否真的是一个需要解决掉的问题。假如我们需要优化一个单参数的函数。如果梯度很小,是不是意味着当前已经在极值附近?所以这其实是一个好消息?类似地,前层的小梯度是不是意味着我们不需要对其做什么调整。
当然,并不是这样。回想一下,我们的网络是随机初始化的,随机初始化的weight和bias不太可能一直都是我们期望的。而且,对于[784,30,30,30,10]网络中的第一层,随机初始化意味着其丢掉了输入图像的大部分信息。即使后层可以很好地训练,但仍然难以辨认原始图像,因为后层只能得到前层没有抛弃的少量信息。
3. 梯度消失的原因
为了探讨梯度消失的原因,我们观察最简单的深度神经网络。如图

图中有三个隐层,使用表示weight,使用表示bias,C是损失函数。使用sigmoid作为激活函数,使用符号表示。
第个neuron的输出,并且 。损失函数C是一个关于的函数。
接下来我们写出的表达式,根据表达式我们会知道梯度消失的原因。

需要注意的是为了方便理解,表达式的每项都与网络对应。
可以看到表达式中除了最后一项,是一系列的乘积。
为了方便,本文称为
我们看一下的函数图像
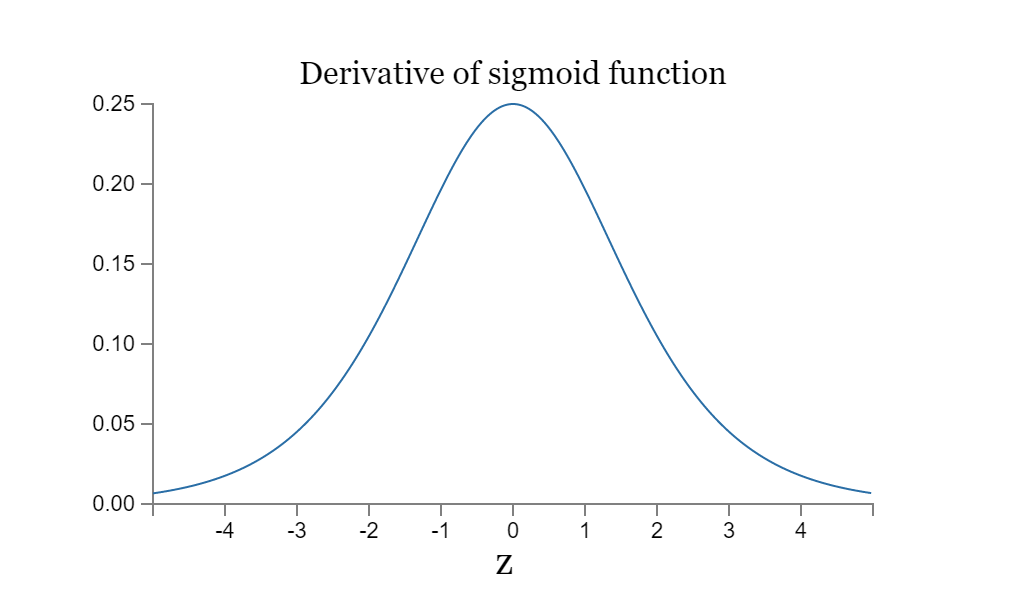
可以看到,其最大值是0.25
通常,我们初始化策略是使用均值为0标准差为1的高斯随机数。
所以weight通常满足
因此,
而这么多个连乘会导致梯度指数降低
为了让这件事情更加清晰,我们比较和
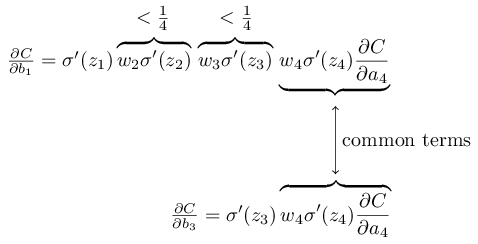
从表达式中可以看出,通常是的16倍。这就是梯度消失的原因。
当然,这是一个非正式的结论,没有严谨地证明梯度消失一定会发生。并且,在训练过程中weight可能会变化,使得。实际上,如果weight变化到使得,随着反向传播的过程,梯度会指数级增长,这时不再是梯度消失问题,而是梯度爆炸问题了。
需要注意的是,本质的原因不是梯度消失和梯度爆炸,而是因为前层的梯度是后续的所有层对应的term的乘积,这使得前层的梯度不稳定,表现为梯度消失或梯度爆炸。